Официальный веб-сайт казино Joycasino предлагает уникальный выбор игровых автоматов от ведущих разработчиков, который стал популярным среди русскоязычных игроков. В казино предусмотрены два режима игры: демо (для ознакомления) и настоящие ставки. Программа лояльности включает многочисленные акции, турниры и розыгрыши. Доступ на официальный сайт казино Joycasino осуществляется через рабочее зеркало 2024.
| Официальный сайт | www.joycasino.com |
| Год основания | 2009 |
| Лицензия | Pomadorro N.V. |
| Способы пополнения | Visa, MasterCard, КИВИ, Биткоин, Альфа-Click, Yandex.Деньги, и другие |
| Способы вывода | Те же, что и для пополнения |
| Программа лояльности | Регулярные розыгрыши, турниры, акции |
| Техническая поддержка | Онлайн-чат (круглосуточно), электронная почта |
| Методы связи с поддержкой | Онлайн-чат, специальный адрес электронной почты (указан в правилах и условиях) |
| Надежность и безопасность | Конфиденциальность данных, лицензия, стандарты |
| Разработчики софта | Microgaming, NetEnt, Playtech, Yggdrasil, и другие |
| Мобильная версия | Да (оптимизирована для смартфонов и планшетов) |
| Валюты | Различные (включая доллары США и российские рубли) |
| Языки | 14 языков (включая русский, английский, и другие) |
| Бонусы | Велком-бонус, бонусы на депозиты, фриспины |
| Категории игр | Слоты, live-дилеры, спорт, live-ставки, джек-поты и другие |
| Минимальный порог для вывода | Не указан (уточняйте на сайте) |
| Отзывы пользователей | Положительные отзывы о разнообразии игр и удобных условиях |
Среди достоинств JoyCasino выделяются различные аспекты. Сначала следует отметить структурированную систему онлайн-платформы, что обеспечивает удобную навигацию для пользователей. Дополнительно, сайт доступен на 14 языках, что удовлетворяет потребности многоязычной аудитории.
Joycasino официальный сайт: обзор казино
JoyCasino официальный сайт — это онлайн-платформа, предоставляющая широкий выбор игровых автоматов и слотов, проверенных многолетним опытом профессиональных игроков. На главной странице сайта представлены виртуальные слоты от различных поставщиков игр по всему миру, доступные как в режиме платных ставок, так и в бесплатном режиме. Для авторизованных игроков разработана специальная бонусная программа, включающая регулярные розыгрыши, турниры и акции.
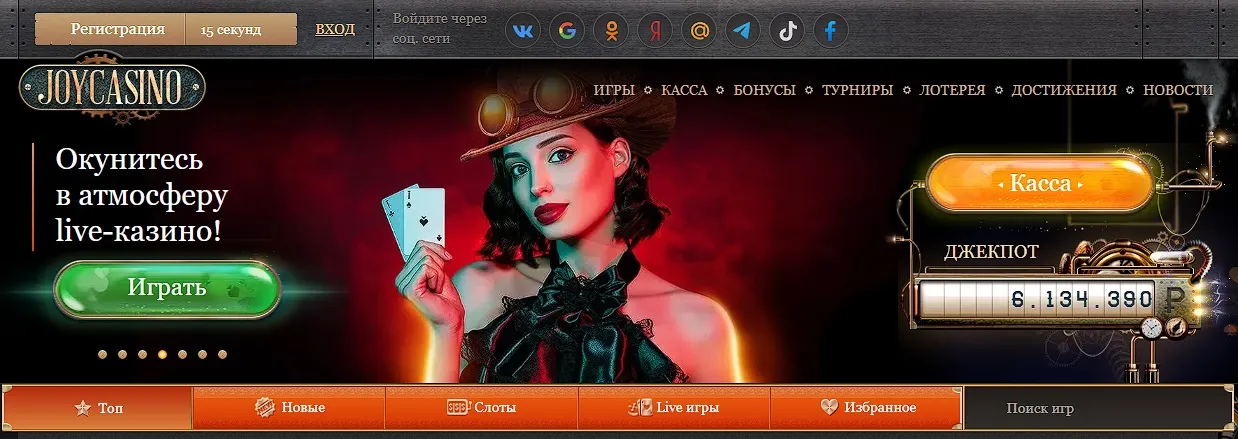
Все услуги Джойказино доступны онлайн через основной сайт, зеркальные страницы, а также предоставляется версия для скачивания. Дизайн главной страницы основан на стиле стимпанк, с использованием различных механизмов и шестеренок, создающих соответствующую атмосферу. Основная цветовая гамма в приятных коричневых оттенках. Интуитивно понятная структура ресурса облегчает навигацию между разделами.
Услуги сайта включают в себя:
- Казино.
- Live-дилеры.
- Спорт.
- Live-ставки.
Для участия в играх на реальные деньги необходимо зарегистрироваться и быть совершеннолетним.
Игровой Ассортимент на Официальном Сайте Joyсasino (Джойказино)
На официальном сайте Joy Casino игроки могут насладиться обширным выбором игровых автоматов и слотов, отобранных на основе многолетнего опыта профессиональных игроков. Главная страница портала приветствует посетителей разнообразием виртуальных слотов от ведущих поставщиков игр по всему миру. Эти игры доступны как в режиме платных ставок, так и в бесплатном режиме, предоставляя игрокам возможность ознакомиться с разнообразием игрового контента до риска настоящих средств.
Уникальный Дизайн и Атмосфера Официального Сайта JoyCasino
Официальный сайт JoyCasino выделяется своим уникальным дизайном, основанным на стиле стимпанк. Использование механизмов, шестеренок и соответствующей цветовой палитры в коричневых оттенках создает уникальную атмосферу, которая добавляет к удовольствию от игры. Интуитивно понятная структура ресурса обеспечивает легкость навигации, позволяя игрокам быстро находить интересующие их разделы и игры.
JoyCasino рабочее зеркало на сегодня 2024: Борьба с блокировками
С постоянными изменениями в политике блокировок интернет-ресурсов, игроки JoyCasino сталкиваются с проблемами доступа. В данном контексте администрация казино оперативно реагирует, предоставляя рабочие зеркала для непрерывного доступа к игровому контенту.
Важность выбора зеркала
Выбор конкретного зеркала не влияет на игровой процесс. Основное требование — стабильное подключение. Игроки могут использовать различные методы обхода блокировок, в том числе и виртуальные частные сети (VPN).
VPN: Эффективный способ обхода блокировок казино Joycasino
Виртуальные частные сети (VPN) – надежный метод обхода блокировок. Позволяют изменять IP-адрес, шифровать соединение и обеспечивать анонимность. Подключение через VPN гарантирует стабильное соединение с JoyCasino.
Преимущества VPN: Надежность и анонимность
Использование VPN для доступа к JoyCasino обеспечивает надежность и стабильность соединения, а также анонимность пользователя. Личные данные защищены, что позволяет игрокам наслаждаться азартными развлечениями, минимизируя трудности с доступом к платформе.
Рекомендации по выбору VPN: Безопасность в приоритете
При выборе VPN важно ознакомиться с политикой конфиденциальности провайдера. Это гарантирует безопасность использования сервиса и поддерживает эффективный доступ к JoyCasino в условиях постоянных блокировок и изменений зеркал.
Регистрация в Джойказино
Существует два метода прохождения этой процедуры:
· указать имя, пароль для входа, свой e-mail, дату рождения, телефон и выбрать валюту;
· выполнить авторизацию через сети «ВКонтакте», «Яндекс», Mail.ru, Google+, Facebook.
Делать депозиты, получать бонусы и подарки, ставить реальные деньги, выводить выигрыши, участвовать в турнирах и акциях можно сразу после прохождения авторизации.
Вход в личный кабинет Joycasino
Для того чтобы начать играть в Joycasino и получить доступ к личному кабинету, вам необходимо выполнить следующие шаги:
- Перейдите на официальный сайт Joycasino.
- Откройте веб-браузер и перейдите на официальный сайт Joycasino.
- Зарегистрируйтесь или войдите в свой аккаунт.
- Если у вас еще нет аккаунта, выполните регистрацию, заполнив необходимые данные.
- Если у вас уже есть аккаунт, нажмите на кнопку «Вход».
- Введите свои учетные данные.
- Введите свой логин (обычно это ваш адрес электронной почты) и пароль.
- Нажмите на кнопку «Войти».
- После ввода данных нажмите на соответствующую кнопку для входа в личный кабинет.
- Личный кабинет Joycasino.
- После успешного входа вы окажетесь в своем личном кабинете, где сможете управлять своим аккаунтом, просматривать историю игр, совершать финансовые операции и получать бонусы.
Играть на реальные деньги в казино JoyCasino
Играть на реальные деньги в JoyCasino — это захватывающий и азартный опыт, который предоставляет игрокам возможность не только наслаждаться увлекательными играми, но и выигрывать реальные суммы. В этом разделе мы рассмотрим ключевые аспекты игры на реальные деньги в JoyCasino.
Преимущества игры на реальные деньги в JoyCasino
- Большие Выигрыши: JoyCasino предлагает игры с высокими коэффициентами выплат, что обеспечивает возможность выиграть значительные суммы денег.
- Широкий Выбор Игр: Казино предоставляет огромный выбор слотов, настольных игр, видеопокера и других азартных развлечений, что позволяет каждому игроку выбирать игры по своему вкусу.
- Бонусы и Акции: JoyCasino радует игроков различными бонусами, лотереями, акциями и турнирами, что увеличивает шансы на выигрыш и делает игру еще более увлекательной.
Шаги для начала игры на реальные деньги
- Регистрация: Создайте аккаунт в JoyCasino, заполнив необходимую информацию. Регистрация обычно проста и занимает всего несколько минут.
- Пополнение Счета: Выберите удобный метод пополнения счета из представленного списка и внесите необходимую сумму.
- Выбор Игры: Перейдите в раздел с играми и выберите ту, которая вам интересна. Удобный интерфейс и категоризация облегчают поиск.
- Ставки и Игра: Установите размер ставки и начните играть. В зависимости от выбранной игры, вы можете использовать различные стратегии и тактики.
- Вывод Выигрыша: После успешной игры, вы можете легко вывести выигранные средства через доступные методы вывода.
Стратегии и советы для игры на реальные деньги
- Управление Банкроллом: Определите заранее, сколько вы готовы потратить, и следите за своим банкроллом. Это поможет избежать неудач и контролировать свои финансы.
- Выбор Игр с Высоким Возвратом: Изучите правила игр и выбирайте те, у которых высокий процент возврата. Это увеличит ваши шансы на выигрыш в долгосрочной перспективе.
- Использование Бонусов: Воспользуйтесь бонусами и акциями, предоставляемыми казино. Это даст вам дополнительные средства для игры.
- Не Забывайте об Отдыхе: Играйте ответственно и не забывайте об отдыхе. Установите себе лимиты и придерживайтесь их.
Игра на реальные деньги в JoyCasino предоставляет уникальный опыт, наполненный азартом и возможностью выиграть крупные суммы. Однако важно помнить о ответственной игре и следовать советам по управлению банкроллом.
Коллекция слотов, игровых автоматов в казино Joycasino
JoyCasino привлекает внимание своей разнообразной коллекцией слотов, игровых автоматов и уникальными развлекательными возможностями. Благодаря этим характеристикам, казино заняло первое место в рейтинге лучших онлайн-казино прошлого года.
Лицензионные игровые автоматы от провайдеров
В JoyCasino представлены только лицензионные игровые автоматы от известных провайдеров. Это гарантирует игрокам высокое качество развлечений и справедливость игры. Позитивные отзывы пользователей подчеркивают комфортные условия, безопасный личный кабинет, значительные призовые фонды и надежную онлайн-кассу.
Разнообразие игрового контента
В арсенале JoyCasino представлен широкий выбор игровых автоматов с высококачественной графикой. Разнообразие жанров удовлетворяет запросы различных игроков, а удобная классификация по группам облегчает поиск интересных игр. Категории включают:
| Категория | Описание |
|---|---|
| Топ | Самые популярные автоматы. |
| Новые | Последние новинки от лучших разработчиков. |
| Слоты | Все слоты с удобным фильтром. |
| Live-дилеры | Настольные и карточные игры с дилером. |
| Джек-поты | 16 игр с розыгрышем джек-пота. |
| Видеопокер | 15 вариаций онлайн-покера. |
| Столы | 59 настольных игр для любителей стратегий. |
| Прочие | 2 игры Flash Track и Sea Raider. |
Удобный поиск и надежность онлайн-казино Joycasino
Поисковая строка обеспечивает мгновенный доступ к любой игре всего в несколько кликов, упрощая процесс навигации и улучшая общий игровой опыт. Казино гарантирует комфортные условия игры, предоставляя игрокам безопасность, высокие призовые фонды и стабильные онлайн-транзакции.
Ведущие разработчики софта
Среди производителей софта JoyCasino выделяются такие известные компании, как Microgaming, NetEnt, Playtech, Yggdrasil, Quickspin, Elk, Playson, Booongo, Red Tiger, TopTrend, Bra Bra Bra, Game Play и многие другие. Это подчеркивает высокий стандарт качества и разнообразие игрового контента на платформе.
Бонусы в казино JoyCasino
Чтобы воспользоваться всеми привилегиями программы лояльности игорного клуба, необходимо зарегистрироваться. Бонус-приветствие ожидает клиентов сразу после авторизации в качестве первого подарка. А при внесении денег на личный игровой счет пользователь сразу получает второй подарок – фриспины.
Приветственный бонус и последующие бонусы на депозиты
Каждый новый пользователь получает приветственный бонус при регистрации:
- 100% бонус до 2000 $ США.
- 150% бонус до 300 $.
- 200% бонус до 50 $.
При внесении второго депозита бонус составляет 100% – до 300 $. За третий – 50% до 400 $. За четвертый депозит – 50% до 500 $. А за пятый депозит – 25% до 750 $.
Фриспины Джойказино
Игроки, которые осуществили депозит на сумму от 1000 рублей, получат вращения бесплатно от казино. Максимальное количество вращений за счет игорного клуба – до двухсот. В течение 10 дней все они будут доступны, по 20 прокруток в сутки.
Мобильная версия сайта казино Joycasino: Играйте в любимые игры на своем iOS или Android устройстве
Мобильная версия казино Joycasino предоставляет удобную возможность играть в азартные игры прямо с вашего смартфона или планшета. Независимо от того, используете ли вы устройство под управлением WinPhone, iOS или Android, вы можете наслаждаться всем разнообразием игр, доступных на официальном сайте.
Особенности мобильной версии:
- Оптимизированные игры:
- Все игры максимально адаптированы для гаджетов, обеспечивая плавную игру без технических замедлений.
- Поддержка различных платформ:
- Joycasino поддерживает устройства с WinPhone, iOS и Android, гарантируя качественный игровой опыт на всех платформах.
- Удобное управление тачскрином:
- Играйте с удовольствием, управляя всем с тачскрина вашего устройства для комфортной навигации и взаимодействия с играми.
Как начать играть через мобильную версию:
- Зайдите с мобильного:
- Откройте сайт Joycasino через мобильный браузер.
- Войдите или зарегистрируйтесь:
- Используйте учетные данные для входа или создайте аккаунт.
- Выберите игру и играйте:
- Откройте раздел игр, выберите слот или настольную игру и начните азартное приключение.
- Управляйте аккаунтом:
- Личный кабинет доступен в мобильной версии. Просматривайте историю игр, осуществляйте финансовые операции и получайте бонусы.
Не упустите возможность насладиться азартными развлечениями Joycasino где угодно. Мобильная версия обеспечивает удобство игры в пути и дает вам контроль над азартным весельем.
Вывод денег и пополнение лицевого счета в казино Joycasino
JoyCasino предоставляет игрокам простые и надежные методы как для пополнения, так и для вывода средств с лицевого счета. Разнообразие вариантов, включая кредитные карты, электронные кошельки и банковские переводы, обеспечивают удобство и гибкость в финансовых операциях.
Популярные методы пополнения и вывода
| Метод | Описание |
|---|---|
| Виза | Карточные платежи от популярной международной системы. |
| МастерКард | Кредитные карты для удобного внесения средств. |
| КИВИ | Электронный кошелек для быстрых транзакций. |
| Биткоин | Криптовалюта для анонимных и безопасных операций. |
| Альфа-Click | Система быстрых онлайн-платежей. |
| Yandex.Деньги | Популярный российский электронный кошелек. |
| Вебмани | Электронная платежная система для мгновенных операций. |
| Skrill | Электронный кошелек с широким функционалом. |
| Сбербанк Онлайн | Интернет-банкинг от ведущего российского банка. |
| Промсвязьбанк | Банковские переводы через популярный банк. |
| Neteller | Электронный кошелек для мгновенных транзакций. |
| Moneta.ru | Российский электронный кошелек для удобных операций. |
| InterKassa | Платежная платформа для различных методов оплаты. |
| WalletOne | Универсальный электронный кошелек. |
| ecoPayz | Глобальный платежный сервис для удобства клиентов. |
| SMS | Пополнение через мобильный телефон. |
| Entropay | Виртуальная карта для безопасных онлайн-платежей. |
Важная информация о верификации
Стандарты безопасности JoyCasino включают процедуру верификации для всех пользователей, запрашивающих вывод средств в размере от 1000 долларов и выше. Эта мера направлена на обеспечение безопасности и соответствия высоким стандартам при проведении операций с крупными суммами. Верификация гарантирует надежность финансовых транзакций и защиту от возможных мошеннических действий.
Техническая поддержка игроков
Онлайн-чат для связи с сотрудниками службы работает круглосуточно, что дает возможность получать ответы на заданные вопросы, не отрываясь от игры.
Вызывает удивление, почему такое популярное и крупное онлайн-казино располагает столь малым количеством методов связи со службой технической поддержки. Конечно, сотрудники помогут игроку, и для таких целей существует не только онлайн-чат: еще один способ – специальный адрес электронной почты, однако найти его не так просто.
Для того чтобы узнать e-mail, надо обратиться к правилам и условиям игорного клуба, которые, как показывает практика, читает малая часть пользователей. Этот серьезный аспект не затрагивается игроками в отзывах о «Джойказино», ведь немало игроков в первую очередь интересуют исключительно халява и бонусы, а на качество услуг глаза закрываются.
Надежность и безопасность
Все личные данные и персональная информация игрока являются конфиденциальными согласно правилам заведения, следовательно, они не могут быть переданы иным лицам. Однако, как и везде, есть исключения: это компании-партнеры казино «Джой-казино». В список попадают сервисы связи (входящих и исходящих вызовов, смс), системы платежей, почтовые сервисы, сервисы чатов онлайн и игровые провайдеры.
Согласно общепризнанным стандартам никакая информация о выплатах игроку и его выигрышах не разглашается. Исключение – официальные запросы от регулирующих органов.
Лицензия
Сайт JoyCasino предоставляет услуги и информацию под контролем компании Pomadorro N.V. Компания обладает соответствующей лицензией, гарантируя игрокам высокие стандарты безопасности и честности. JoyCasino является лицензированным оператором, что подчеркивает его стремление соблюдать все необходимые стандарты в индустрии азартных игр. Подтверждение лицензии обеспечивает честную и безопасную игровую среду для игроков.»
Плюсы и минусы ДжойКазино
Джойказино – крупная онлайн-игорная площадка, предлагающая разнообразные видеослоты, настольные и карточные игры, а также игры с живыми дилерами круглосуточно.
Плюсы:
- Возможность бесплатной активации всех автоматов, кроме лайв-моделей, без регистрации и смс-переводов.
- Удобные системы платежей и сотрудничество с мировыми разработчиками программного софта.
- Специальная программа для зарегистрированных пользователей: бонусы, турниры и акции.
- Версия для смартфонов и планшетов с детальной оптимизацией игры.
- Минимальный порог для вывода средств, доступный каждому игроку.
Минусы:
- Меню с акциями и турнирами могло бы быть более заметным.
- Электронная почта службы поддержки размещена глубоко в соглашении с пользователем.
Несмотря на небольшие недостатки, «JoyCasino» заслуживает признание как лидер в индустрии азартных игр, обеспечивая игрокам разнообразие игр и удобные условия игры на деньги.
Часто задаваемые вопросы про казино JoyCasino
Для регистрации в казино Joycasino пройдите на официальный сайт, нажмите на кнопку «Регистрация» и следуйте инструкциям, предоставив необходимую информацию.
Joyсasino предоставляет разнообразные методы пополнения, включая кредитные карты, электронные кошельки (Yandex.Деньги, Skrill, WebMoney и др.), биткоин, банковские переводы и другие.
Для вывода выигранных средств выберите удобный метод вывода из списка доступных. Важно пройти верификацию, если запрошенная сумма достигает установленного порога.
Да, JoyCasino обеспечивает возможность игры на мобильных устройствах через мобильную версию сайта или скачиваемое приложение, обеспечивая удобство игры в любом месте.